Matrix
K-Nearest Neighbor is the one of the well-known and easy machine algorithm which is very suitable for a lot of real-world problems such product recommendation, social media friend recommendation based on interest or social network of person.
2 Rows 3 Columns Matrix
Matrixes are very useful while we are working on machine learning algorithms, assume that we have 1000 data with 10 features for each row, by using matrix structure we can easily handle this data and access any member of it according to requirements, such data can be defined as 1000 rows 10 columns.
Adding
We can add two equal matrices (both matrices has to be same sizes of rows and columns).
While adding one matrix to another one, the rule is computing each row of the first matrix to the same row of the second matrix (as position), it is same for columns as well.
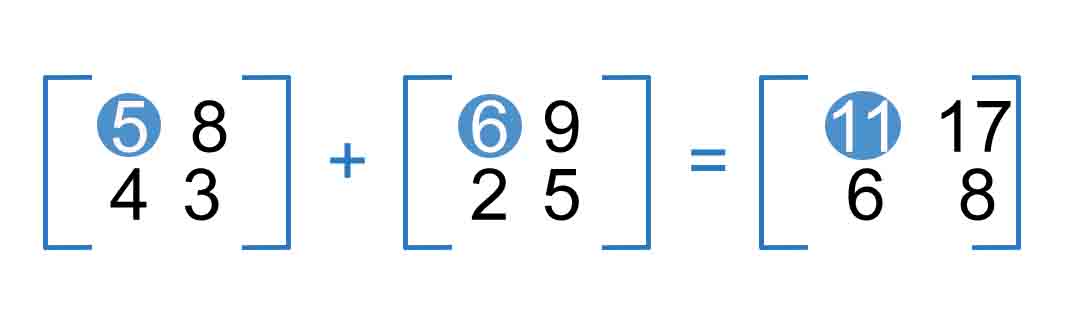
These are the calculations:
5+6 = 11 4+2 = 6
8+9 = 17 3+5 = 8
Subtracting
We can subtract two equal matrices from each other (both matrices has to be same sizes of rows and columns). We can define as addition of a negative matrix: Matrix1 + (−Matrix2)
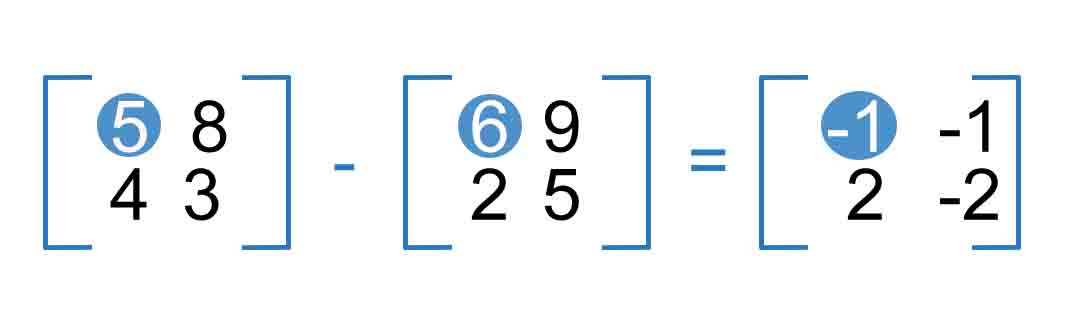
These are the calculations:
5-6 = -1 4-2 = 2
8-9 = -1 3-5 = -2
Multiply
Multiplying has some additional points to pay attention when we want to multiply a matrix with the constant it is pretty simple (called scalar multiplication), but when we want to multiply a matrix by another matrix, we need to use dot product.
Multiply by Constant
Simply we multiply constant with each row and column of the matrix.
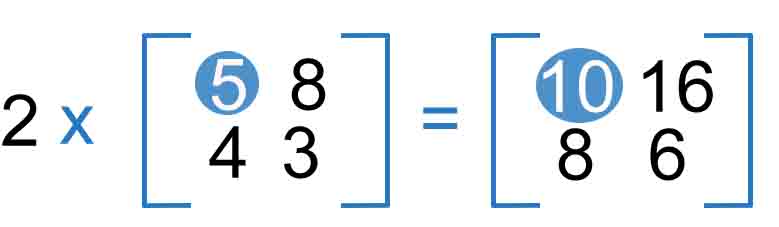
These are the calculations:
2x5 = 10 2x4 = 8
2x8 = 16 2x3 = 6
Multiplying a Matrix by Another Matrix
Here, we need to use dot product to be able to multiply a matrix by another matrix
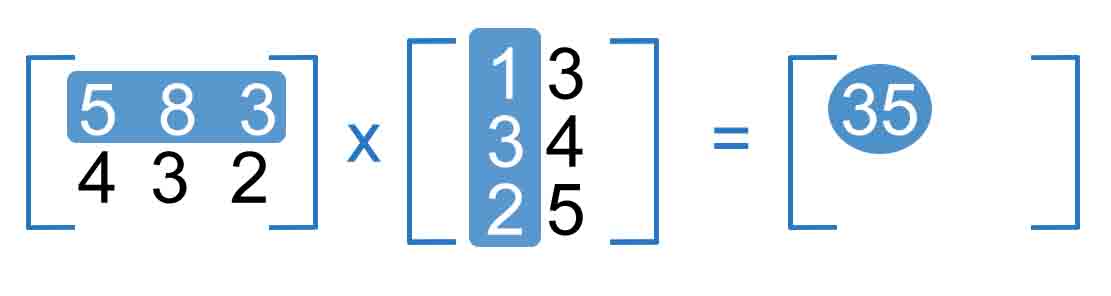
These are the calculations:
(5x1) + (8x3) + (3x2) = 35
Multiplying the first row with all its columns of the first matrix by the first column of the second matrix with the all its rows and sum up all will give us first column of the first row of the result matrix.
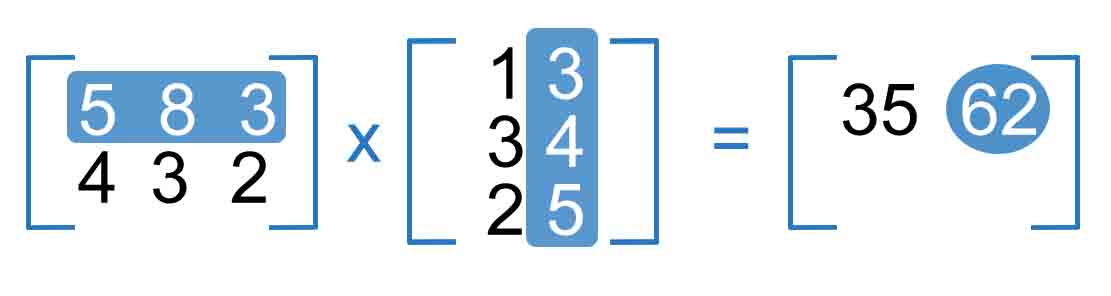
These are the calculations:
(5x3) + (8x4) + (3x5) = 62
By continuing to do this as multiplying the first row with all its columns of the first matrix by the second column of the second matrix with the all its rows and sum up all will give us the second column of the first row of the result matrix.
With the same logic we can continue to multiply the second row of the first matrix by each column and its all rows of the second matrix, and then sum up will give us the second row of the result matrix with all columns of it.
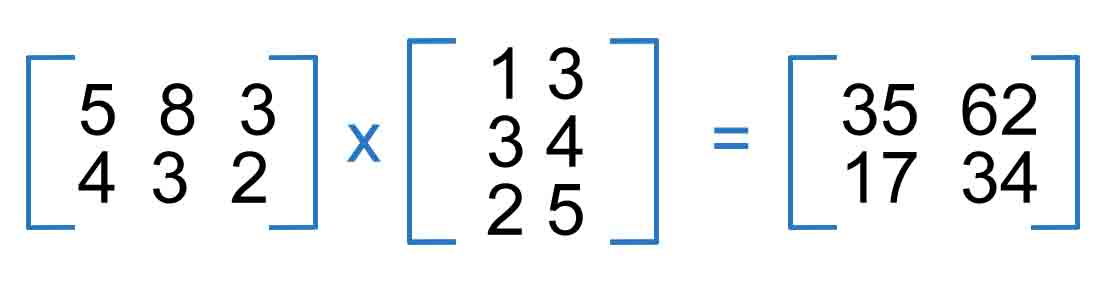
Inverse
The inverse of the matrix is the same idea with reciprocal of a Number, the difference is we write it as A-1.
Please note that sometimes it is possible that matrix does not have the inverse.
Determinant of 2x2 Matrix
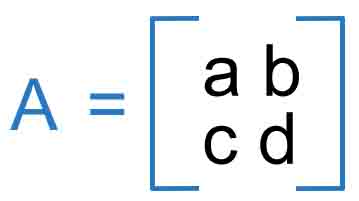
We can simply say that the determinant of A equals a times d minus b times c.
Inverse of 2x2 Matrix
As you can see below, swapping the position of a and d and putting negatives in front of b and c and divide everything by the determinant will give use inverse matrix.
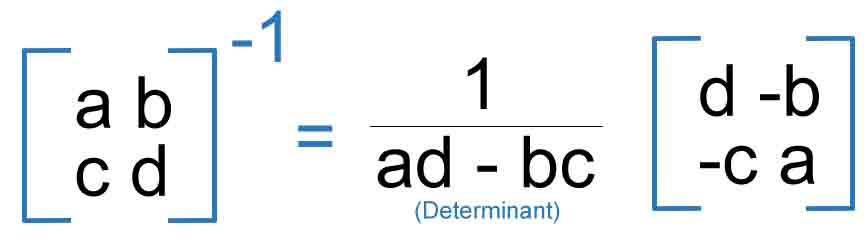
Dividing
Actually, for matrixes, there is no dividing, instead of dividing matrix, we get inverse and multiply by it.
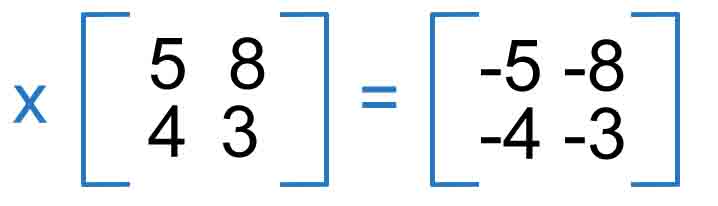
Negative
Negative of a matrix is pretty simple, we multiply each column of the row by “-” to find rows and columns of the result matrix.
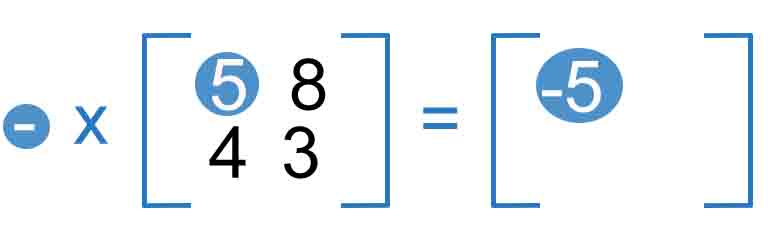
These are the calculations:
- x (5) = -5 - x (8) = -8
- x (4) = -4 - x 3 = -3
Transposing
We call swapping the rows and columns as "transpose" a matrix.
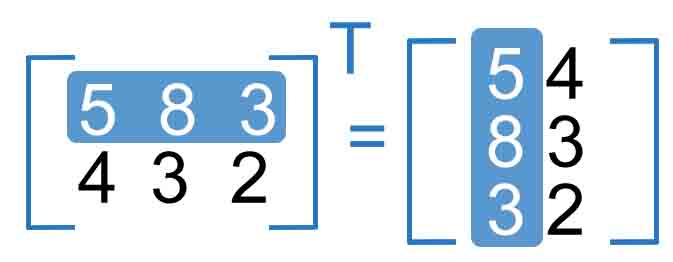
“T” is the symbol of the “transpose”
Thanks for reading.